Датировка каталога Улугбека методом Дамбиса-Ефремова
М. Маркабов
В работе А.К. Дамбиса и Ю.Н. Ефремова "Датировка звездного каталога Птолемея
по собственным движениям: тысячелетняя проблема решена" [1] проведена попытка
датировки звездного каталога "Альмагест" разработанным авторами "коллективным
методом". В результате расчетов, авторами была получена дата составления
каталога "Альмагест" Tλβ=-89 год при погрешности в 122 года. Этот
результат позволил А.К. Дамбису и Ю.Н. Ефремову сделать заключение, что звездный
каталог "Альмагест" был составлен во времена Гиппарха и исключить авторство
Птолемея с вероятностью 94%. В этом тезисе и состояло "решение тысячелетней
проблемы", о котором было заявлено в заглавии статьи.
Заявление о возможности
определения принадлежности авторства каталога оказалось столь интересным, что
работа А.К. Дамбиса и Ю.Н. Ефремова была перепроверена Д. Дьюком [2]. Деннис
Дьюк перепроверил датировку каталога "Альмагест" методом Дамбиса-Ефремова и
пришел к выводу, что из-за некорректного учета ошибок, реальная погрешность
датировки каталога значительно выше. Более высокое значение погрешности метода
делает невозможным уверенно приписать авторство каталога Гиппарху или Птолемею,
поэтому заявление А.К. Дамбиса и Ю.Н. Ефремова об авторстве Гиппарха является
несостоятельным.
Однако, вопрос о результатах датировки каталога "Альмагест"
"коллективным методом" в исполнении А.К. Дамбиса и Ю.Н. Ефремова нельзя считать
полностью закрытым по двум причинам. Во-первых, предложенный авторами
"коллективный метод" датировки звездных каталогов является новым и не
апробирован на других звездных каталогах авторство и датировки которых не
вызывают сомнения. Во-вторых, при построении регрессии, авторы почему-то
полагают, что ошибки в окрестностях всех звезд одинаковы, что заведомо ошибочно.
В связи с этим возникает сомнение, что предложенный А.К. Дамбисом и Ю.Н.
Ефремовым "коллективный метод" в принципе способен обеспечивать адекватный
результат датировки.
Для решения этого принципиального вопроса, мы провели
апробацию "коллективного метода" на звездном каталоге Улугбека [3], который
датируется 841 годом Хиджры, что соответствует 1437 году нашей эры. Среди других
средневековых каталогов, каталог Улугбека был выбран по той причине, что он
имеет одинаковый состав быстрых звезд и похожее значение случайной ошибки
измерения.
Методика датировки звездных каталогов Дамбиса-Ефремова
Кратко опишем методику, предложенную А.К. Дамбисом и Ю.Н. Ефремовым в работе
[1]. Предположим, звездный каталог был составлен в некий год Т. Используя
современный высокоточный звездный каталог, формулы прецессии и учитывая
собственные движения звезд, вычислим истинные эклиптические координаты λ и δ
всех звезд исследуемого каталога на некий год Т. Для каждой звезды каталога
определим невязки координат Δλ и Δβ как разницу значения величины, взятой из
датируемого каталога и расчетной величиной на дату Т:
Вокруг каждой звезды с большим собственным движением (обозначаем символом *), выделим группу из нескольких ближайших звезд сравнения Nnei и определим систематическую ошибку этой окрестности в долготе и в широте из значений невязок звезд сравнения. Систематическую ошибку авторы определяют не усреднением, а по медиане, что позволяет исключать выбросы.
Δλ* cos β* - < Δλnei cos
βnei> = (1/60)(μλ* - <
μλnei>) Tcat +
Δλ'*acos β (1)
Δβ*
- <Δβnei> = (1/60)(μβ* - <
μβnei>) Tcat + Δβ
'*a (2)
где μλ и μβ - проекции собственного движения по долготе и широте в секундах дуги в год; коэффициент 1/60 преобразует собственное движение из секунд в год к минутам в год; Tcat - возраст каталога, отсчитываемый от предполагаемой даты составления Т; Δλ'*a и Δβ'*a - случайные ошибки измерения, которые неизвестны. Общая идея метода продемонстрирована авторами на рис. 1.

Рис. 1. Разность координат, приведенных в "Альмагесте" и вычисленных на эпоху первого года до н.э. (минус средняя такая разность для шести ближайших медленных звезд), в зависимости от соответствующей компоненты собственного движения для 50 самых быстрых звезд "Альмагеста".
По оси абцисс откладывается компонента собственного движения быстрой звезды μλ, β* за вычетом средней скорости окрестности <μλ, βnei>, по оси ординат откладывается разность невязок быстрой звезды и усредненной невязки окрестности Δλ или Δβ для данной компоненты скорости. Из дальнейшего рассмотрения исключаются точки у которых значение Δλ или Δβ превышает утроенную среднеквадратичную ошибку. Далее, через оставшееся множество точек методом наименьших квадратов проводится прямая типа y=kx откуда определяется тангенс наклона k. Отсюда, дата составления каталога определится как Tcat = T + 60• k, а погрешность датировки определится через погрешность тангенса угла наклона как ΔT = 60•Δk. Решая отдельно систему уравнений для долгот (1) и широт (2) авторы получают две датировки Tλ и Tβ вместе с ошибками σTλ и σTβ, а так же средними случайными ошибками Δλ'*a и Δβ '*a. Решая совместно систему уравнений (1) и (2) с весами, обратно пропорциональными σλ'*a и σβ'*a авторы получают уточненную датировку Tλβ.
Весьма существенным в методике датировки Дамбиса-Ефремова является выбор
числа звезд сравнения окрестности. Авторы решают этот вопрос следующим
образом:
Мы применили описанный в предыдущей главе метод
ко всему каталогу "Альмагест" или точнее, к 1020 его звездам, исключив
предварительно четыре повторных записи и четыре незвездных объекта. Далее мы
получили датировки каталога, используя все возможные комбинации параметров
Nnei = 2,...21 и Nfast = 11,...100 (т.е., используя от 11
до 100 самых быстрых звезд от 2 до 21 ближайших опорных звезд для каждой быстрой
звезды). При этом опорные звезды отбирались по их близости к быстрой звезде
согласно координатам "Альмагеста", чтобы этот выбор не зависел от начальной
эпохи (в нашем случае - первый год до н.э.). Для начала надо выбрать оптимальное
число опорных звезд Nnei для каждой быстрой звезды. Это, очевидно,
такое число опорных звезд, которое позволяет спрогнозировать систематическую
ошибку координатной разности с наибольшей точностью. Эффективность такого
прогноза измеряется среднеквадратичной ошибкой соответствующей координаты,
определяемой путем решения систем уравнений (9) и (10) [в нашей нумерации (1) и
(2) - Авт.] методом наименьших квадратов: σλ' = σ(Δλ • cos β • -
<Δλnei cos β r>) и
σβ= σ (Δβ * - <Δβnei>).
На рис.2 и рис.3 показан алгоритм выбора оптимального числа звезд окрестности Nnei и количества быстрых звезд Nfast.

Рис. 2. Местные среднеквадратичные случайные ошибки σλ и σβ эклиптических координат Nfast = 100 самых быстрых звезд "Альмагеста" в зависимости от числа используемых соседних опорных звезд Nnei. Видно, что ошибки обеих координат перестают уменьшаться при Nnei>6.

Рис. 3. Среднеквадратичная ошибка sTλβ, совместной датировки по широтам и долготам в зависимости от числа Nfast используемых самых быстрых звезд "Альмагеста". Для каждой быстрой звезды использовалось по Nnei=6 медленных опорных звезд. Видно, что ошибка датировки остается практически постоянной после того, как число быстрых звезд превысит 40.
Таким образом, при определении датировки каталога авторы использовали 40 быстрых звезд, а окрестность сравнения относительно которой проводилась оценка положения быстрой звезды состояла из 6 звезд. В результате были получены следующие датировки Tλ= -110 ±230; Tβ = -80 ±150; Tλβ= -90 ±120, а среднеквадратичные ошибки эклиптических координат составила σλ = 18' и σβ = 13'.
Замечания к методике Дамбиса-Ефремова
Несмотря на кажущуюся проработанность способа датировки Дамбиса-Ефремова авторы делают ряд существенных упрощений и неоговоренных допущений, которые делают работу методологически не состоятельной. Сформулируем основные замечания.
Замечание 1. Серьезным недостатком методики является удаление
информации о случайных ошибках измерения в окрестности быстрой звезды расчета
датировок Tλ и Tβ. В самом деле, в уравнениях для долготы
и широты:
Δβ* - <Δβnei> = (1/60)(μβ* - < μβnei>) Tcat + Δβ '*a
последние члены, имеющие смысл случайных ошибок измерения (выделенны красным)
просто приравниваются к нулю. То есть, высота точки по оси абцисс полностью
приравнивается первому правому члену уравнения, которое описывает собственное
движение звезды. При определении наклона регрессии, используется информация
только о разности проекции скорости быстрой звезды и окрестности (ось Х), и
разности скорости быстрой звезды и средней скорости окрестности (ось Y).
Случайные ошибки измерения в эти величины не входит. Здесь А.К. Дамбис и Ю.Н.
Ефремов делают сразу два допущения, они полагают что ошибка измерения во всех
окрестностях одинакова и равна нулю. В принципе, ход авторов понятен, поскольку
одно уравнение с двумя неизвестными может не иметь однозначного решения. Однако,
значение величины случайной ошибки измерения значительно отличается в разных
окрестностях, что очень просто устанавливается по ошибкам звезд окрестности (к
этому вопросу мы вернемся ниже). Поэтому сами величины Tλ и
Tβ определены неправильно и с заниженными значениями погрешности.
Авторы как бы вспоминают о членах уравнений Δλ'*acos β и
Δβ '*a только после определения независимых датировок по
проекциям Tλ, Tβ и используют их при вычислении смешанной
датировки Tλβ.
Эффективность работы предложенных авторами поправок
можно очень просто проверить. Проведя регрессию сразу по всем точкам (и
долготным, и широтным) мы вычислили датировку Tλβ без определения
промежуточных датировок по проекциям Tλ, Tβ не используя
никакие веса, рис. 4. Кроме того, мы не вычитали из проекции собственной
скорости звезды усредненную проекцию скорости окрестности, поскольку для
подавляющего большинства быстрых звезд такая поправка ничтожна.

Рис. 4. Вычисление датировки смешанной Tλβ без расчета частных датировок Tλ и Tβ
В результате вычисления был получен коэффициент регрессии k=-1.41 ± 2.07, что в пересчете дает календарную дату -85 год ±124 года. что почти не отличается от результата А.К. Дамбиса и Ю.Н. Ефремова -89 год ±122 года. Это означает, что предложенная авторами методика расчета смешанной датировки Tλβ, в которой по замыслу авторов должна учитывать индивидуальную ошибку в координатах звезды, дает такой же результат, когда смешанная датировка по широтам и долготам вычисляется напрямую без поправок. Следовательно, данная методика не эффективна.
Замечание 2. Методика выбора числа звезд окрестности предложенная авторами при первом же рассмотрении не работоспособна и не в состоянии выделить оптимальное число звезд сравнения. Действительно, на рис.2 при Nref=6 наблюдается минимум в локальной погрешности долготы и широты, однако, оба эти минимума статистически неразличимы, рис. 4.

Рис. 5. Локальные среднеквадратичные случайные ошибки σλ и σβ эклиптических координат Nfast = 100 самых быстрых звезд "Альмагеста" в зависимости от числа используемых соседних опорных звезд Nnei.
Из рисунка видно, что значение локальной погрешности в долготе
σλ(Nref=6) составляет около 18.5'. Но вместе с этим, локальная
погрешность существенно не изменяется при Nref от 4 до 21 звезд,
когда σλ составляет около 19' и отклоняется от этой величины менее чем на 1' при
разных значениях Nref. Поскольку само значение σλ определено с
точностью не лучше чем 5÷10% от значения величины, локальный минимум при
Nref=6 выделить невозможно. Кроме того, можно выделить еще два
локальных минимума при Nref=4 и 13, причем последний минимум это
самый глубокий минимум из этой тройки. С другой стороны, с потерей точности в 2'
можно использовать даже три звезды сравнения.
Та же самая ситуация
наблюдается с зависимостью локальной ошибки в широте σβ от Nref. При
этих же значениях Nref величина локальной ошибки σλ составит около
16' и изменяется на всем интервале менее чем на 1'. Однако, значение σβ так же
определено с погрешностью около 1', поэтому, достоверно вычислить оптимальное
число Nref на основании представленной зависимости невозможно.
Таким образом, на основании представленной методики выбора Nref невозможно статистически определить оптимальное число звезд сравнения. Возможная причина этого состоит в том, что окрестности звезд сравнения очень разные и следовало бы искать не универсальное значение Nref, которое применяется абсолютно ко всем окрестностям быстрых звезд, а предложить прозрачно работающий алгоритм, который автоматически определял бы Nref для каждой окрестности.
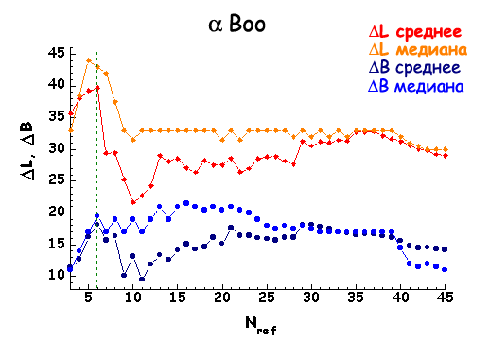
Замечание 3. Вернемся к вопросу об ошибках в окрестностях быстрых звезд. Для этого, рассмотрим как изменяется ошибка в окрестности быстрой звезды в зависимости от числа Nref, рис.6.
 |
 |
 |
 |
Рис. 6. Функции невязок координат в окрестностях ο2 Eri, α Boo, τ Cet и α CMa.
Из представленных рисунков видно, что усредненные невязки звезд сравнений различным образом ведут себя в окрестности Nref=6. Например, невязки определенные по медиане устойчивы по долготе у Кейда (ο2 Eri), Арктура (α Boo), τ Cet и по широте у Сириуса (α CMa). Поэтому, для таких окрестностей вполне возможно использование единого значения Nref от 3 до 10. И наоборот, широтные невязки медленных звезд окрестностей Кейда, τ Cet и долготная невязка окрестности Сириуса неустойчивы значительно изменяются в зависимости от Nref. Например, ошибка окрестности Кейда при Nref=4 и Nref=8 изменяется на 16', ошибка окрестности τ Cet при переходе от Nref=6 к Nref=10 изменится на 16', а ошибка окрестности Сириуса изменяется на 12' при переходе от Nref=4 к Nref=6. Заметим, что неустойчивость в рассмотренных окрестностях наступает при разных значениях Nref, поэтому корректно определить для таких окрестностей единое число звезд сравнения нельзя.
Вернемся к вопросу выбора оптимального числа быстрых звезд Nfast и звезд сравнения Nref рис.2, рис.3. Из последнего рисунка авторы делают вывод, что погрешность датировки перестает существенно изменяться при Nfast=40, поэтому и используют это число в дальнейших расчетах. Теперь, после разбора невязок звезд сравнения Кейда, Арктура, τ Cet и Сириуса становится совершенно понятно почему функции локальной погрешности от Nref практически не зависят от числа звезд сравнения на значительном интервале Nref. Часть окрестностей устойчива от Nref (незначительно изменяется при изменении числа звезд сравнения), поэтому в них можно брать различное Nref. К этим окрестностям подмешиваются неустойчивые окрестности, в которых локальная ошибка может изменяться на десятки минут при небольшом изменении Nref. Но если неустойчивых окрестностей много, их вклад в общую локальную ошибку усредняется, поэтому функции локальных ошибок на рис. 2 не имеют ярко выраженных минимумов. Если бы авторы вычислили функции локальных ошибок от Nref для большего числа быстрых звезд, например, Nfast=60 или 80, функции локальных ошибок еще меньше зависели бы от Nref. И наоборот, при меньшем числе быстрых Nfast звезд зависимости локальных ошибок от Nref были бы выражены сильнее, правда значение Nref может оказаться другим и неединственным.
В завершении, выскажем к рис. 3 еще одно небольшое, но существенное замечание. При изменении значения Nfast от 10 до 11 происходит резкое (в несколько раз) уменьшение погрешности датировки. Это не понятный результат, поскольку значения функций локальных ошибок при этом изменяются слабо, а вклад от одной быстрой звезды (в данном случае η Cas) незначителен.
Замечание 4. Частное замечание. Применение единого значения
Nref в разряженных окрестностях или небольших созвездиях в ряде
случаев заведомо выводит за пределы области одинаковых систематических
ошибок.
Например, звезда δ Треугольника имеет высокую скорость по долготе
(+0.93 "/год) и широте (-0.63 "/год) и представлена сразу двумя значимыми
точками. Однако, созвездие Треугольника в каталоге "Альмагест" содержит всего
четыре звезды, одна из которых быстрая, поэтому при Nref=6 оставшиеся
три звезды сравнения приходится брать из соседних созвездий, которые имеют
совсем другую систематику. Вычислим невязки координат медленных звезд
окрестности δ Треугольника на -1 год н.э.
| № | Байли | Байер/Флемстид | Δλ•cos β | Δ β |
| 1 | 359 | β Tri | -36' | -13' |
| 2 | 361 | γ Tri | -14' | -12' |
| 3 | 358 | α Tri | -58' | +16' |
| 4 | 219 | 16 Per | +9' | +9' |
| 5 | 349 | γ And | +26' | -21' |
| 6 | 377 | 39 Ari | +2' | -18' |
| 7 | 378 | 35 Ari | +19' | -2' |
В данном случае, в окрестность звезд сравнения берутся три звезды из трех
разных созвездий, которые имеют разные групповые ошибки. Если в широте ошибки
звезд 219, 349 и 377 примерно соответствуют ошибкам звезд контура созвездия
Треугольника, то долготные ошибки добавленных звезд имеют совсем другую
систематику, что неизбежно сказывается на датировке. В самом деле, если
определить окрестность по трем ближайшим звездам, то ошибка окрестности в
долготе составит -36' по медиане и -33' по среднему. В окрестности составленной
из 6 ближайших звезд, долготные ошибки окажутся равными -6' по медиане и -12' по
среднему, то есть изменятся относительно предыдущего результата на 20'÷30'. Это
качнет датировку на полторы тысячи лет.
Проведем еще один эксперимент,
заменим последнюю звезду окрестности 377(=39 Ari) следующей по близости звездой
378 (=35 Ari), которая удалена от δ Треугольника примерно на 0.5° дальше, чем
377. Звезда 35 Овна имеет невязки в долготе и широте соответственно (+19';-2'),
что еще хуже соответствует ошибкам звезд Треугольника и приведет к еще большей
ошибке.
Таким образом, когда быстрая звезда находится в разряженной
окрестности и окрестность доукомплектовывается ближайшими звездами соседних
созвездий, ошибка окрестности может изменяться самым непредсказуемым
образом.
| № | Байли | Байер/Флемстид | Δ β |
| 1 | 31 | ν UMa | 13' |
| 2 | 490 | 54 Leo | 55' |
| 3 | 481 | δ Leo | 37' |
| 4 | 489 | 41 LMi | 32' |
| 5 | 30 | ψ UMa | 11' |
| 6 | 495 | 15 Com | -15' |
| 7 | 480 | 60 Leo | 33' |
Из представленной таблицы следует, что в окрестность сравнения ξ Большой Медведицы набраны звезды с совершенно разными ошибками. Звезды 481, 489 и 490 имеют свою систематическую ошибку, которая характерна для созвездия Льва. Звезда 495 так же относится в "Альмагесте" ко Льву, но имеет свою ошибку, отличную от ошибки всех остальных звезд окрестности. Замена этой звезды чуть более удаленной 480 (60 Leo) ухудшает ситуацию еще сильнее - в этом случае движение ξ Большой Медведицы оценивается по звездам созвездия Льва 480 и 489. Было бы разумным предположить, что координаты ξ UMa измерялись вместе со звездами Большой Медведицы, а не Льва, поэтому систематическая ошибка составленной таким методом окрестности не имеет никакого отношения к этой звезде.
Замечание 5. О распределении ошибок в окрестностях. Авторы вычислили,
что оптимальное значение Nref для звездного каталога "Альмагест"
равно 6, откуда по медиане были вычислены групповые ошибки окрестности в долготе
<Δλnei и в широте <Δβnei>. Преимущество
использования метода расчета ошибке по медиане состоит в том, что в отличии
расчета ошибки по среднему, этот метод позволяет эффективно устранять выбросы.
Однако, использование медианы дает корректный результат только в том случае,
когда ошибки в окрестности распределены по закону Гаусса. Авторы не изучают
вопрос распределения ошибок в окрестностях, по крайней мере, если какое-то
исследование в работе [1] и проводилось, то оно никак не отражено. Ошибки в
окрестности быстрой звезды не обязательно должны подчиняться распределению
Гаусса, но даже в идеальном случае, при небольшом числе (Nref=6) проб
(опорных звезд или звезд сравнения) распределение ошибок будет заведомо
отличаться нормального распределения. В том случае, когда в окрестности
присутствуют выбросы (которые можно представить как ступеньку в распределении),
Nref уменьшится и форма распределения еще сильнее будет отличаться от
нормального распределения. В случае малого числа испытаний, более точно форму
распределения описывает распределение Стъюдента, однако в этом случае будет
получена менее точная оценка случайной ошибки измерения.
Таким образом,
заменяя реальные распределения ошибок на нормальные, авторы вносят трудно
оцениваемую ошибку, которая сказывается на центре датировки, так и на
погрешности датировки.
Замечание 6. Во всех предыдущих рассуждениях ставилась задача
выделения окрестности быстрой звезды, которая имеет одинаковую с быстрой звездой
групповую ошибку. При этом предполагалось, что разброс индивидуальных невязок в
группе звезд сравнения целиком определяется случайной ошибкой измерения. Однако,
это предположение справедливо далеко не всегда, поскольку в протяженных
окрестностях к случайным ошибкам измерения добавляются систематические ошибки.
Например, окрестность Сириуса является компактной и нужные 6 звезд сравнения
набираются на радиусе около 5° от звезды. В данном примере, даже если звезды
сравнения находятся диаметрально противоположно, систематическая ошибка будет
крайне мала. С другой стороны, в окрестности звезды τ Cet, 6 звезд сравнения
набираются при радиусе окрестности около 11°, при этом, угловое расстояние между
крайними звездами окрестности σ и η составляет 21°, а их удаленность от самой τ
Cet превышает 10°. Во-первых, в этом случае, нет оснований считать, что все эти
звезды измерены при настройке астролябии по одной опорной звезде (в противном
случае групповые ошибки могут априорно отличаться поскольку разные опорные
звезды могут иметь собственные ошибки в координатах, которые наследуются всеми
промеренными окрестностями) и, что координаты этих трех звезд были измерены за
один сеансе настройки по опорной звезде (поскольку сама процедура настройки
прибора на опорную звезду происходит с какой-то ошибкой). Следовательно, эти
звезды могут иметь совершенно разные ошибки и объединять их в одну окрестность
не правомерно.
Во-вторых, дополнительную ошибку в протяженную окрестность
вносит систематическая ошибка. Например, авторы [4]÷[6] оценивают разницу
наклона плоскости эклиптики "Альмагеста" от расчетной от γ=18' до 21'. Это
означает, что крайние звезды окрестности радиусом 10° будут иметь разную
систематику до γ•sin20°=7'. В принципе, это не очень большая величина по
сравнению со случайной ошибкой измерения ~20', тем более, когда групповая ошибка
окрестности считается по широте. Но тем не менее, эта ошибка не учитывается и не
оказывает по мнению авторов влияния ни на саму датировку, ни на ошибку к
ней.
Если же быстрая звезда движется по долготе, и групповую ошибку
окрестности нужно так же искать по долготе, то можно игнорирование систематики
может привести к огромным ошибкам. В качестве примера, можно привести звезды 57
(Байли=σ Dra) и 61(χ Dra), которые расположены на высоких широтах. Окрестность σ
Dra при Nref=6 состоит из 55(ε Dra), 58(υ Dra), 59(τ Dra), 54(δ Dra),
56(ρ Dra) и 53(π Dra), a радиус окрестности составляет около 5°. Однако, часть
звезд этой окресности удалена друг от друга по долготе на десятки градусов.
| Байли | Байер/Флемстид | Долгота 1 г. н.э. |
| 53 | π Dra | 337° |
| 54 | δ Dra | 350° |
| 55 | ε Dra | 6° |
| 57 | σ Dra | 10° |
| 58 | υ Dra | 24° |
| 59 | τ Dra | 28° |
Учитывая, что в долготах звездного каталога "Альмагест" присутствует примерно такая же сиcтематическая ошибка, как и в широтах [5], наличие систематики обеспечит ошибку на разных звездах до 15'÷20'. Поэтому, предположение о том, что в данном случае звезды набранной окрестности имеют единую групповую ошибку является заведомо неправильным. Точно такая же ситуация происходит в окрестности быстрой звезды χ Дракона, которая так же расположена на высокой широте, а движется по долготе. Тем не менее, авторы не делают поправки на систематику ни для одной окрестности.
Заключение.
Сформулированные замечания разнообразны по своему характеру и касаются как самых общих методических вопросов связанных с определением оптимального числа звезд сравнения и учета систематических ошибок, так и частных замечаний, которые ставят под сомнение правильность вычисления датировок по отдельным звездам. По отдельным звездам датировка была омоложена, по другим удревнена, методика выбора числа звезд сравнения оказалась не работоспособной, систематические ошибки в окрестностях не учтывались в принципе, а единственная попытка учета случайной ошибки на этапе вычисления смешанной датировки Tλβ оказалась неудачной. Сформулированные недочеты методики датировки предложенной А.К. Дамбисом и Ю.Н. Ефремовым позволяют утверждать, что погрешность используемого ими метода значительно больше заявленной авторами точности и не способна отличить эпоху Гиппарха от эпохи Птолемея. Это заключение находится в соответствии с выводом работы Д.Дъюка [2], который повторил методику авторов при датировке звездного каталога "Альмагест".Наш предварительный вывод состоит в следующем. Коллективный метод А.К. Дамбиса и Ю.Н. Ефремова имеет погрешность датировки до нескольких раз выше заявленной, при этом центр датировки может вычисляется со значительными отклонениями от реальной даты составления каталога. Для подтверждения этого тезиса применим "коллективный метод" для датировки каталога Улугбека, который имеет примерно такую же точность измерения координат и состав быстрых звезд.
Исследование ошибок в каталоге Улугбека
Для расчета звездного неба в прошлое, воспользуемся современными данными о
координатах и проекциях скоростей звезд [7] и алгоритм расчета координат звезд
изложенный в [8],[9], который учитывает прецессию и собственное движение
звезды.
Определим расчетные эклиптические координаты звезд, которые
содержатся в каталоге Улугбека на 1437 год и сравнив их с координатами звезд
каталога, определим невязки в долготе и в широте для каждой звезды. Исключим из
дальнейшего рассмотрения все звезды у которых абсолютные значения невязок
превышают 120'. Кроме того, автоматически исключим из дальнейшего рассмотрения
27 южных звезд, которые согласно свидетельству Улугбека были заимствованы им из
работы ас-Суфи.
Для определения систематических ошибок построим зависимости
распределений долготных и широтных невязок от долготы и апроксимируем полученное
распределение ошибок функцией типа ΔSλ;b =
γλ;b•sin(L-φλ;b) откуда определим искомые значения
γλ;b, φλ;b и погрешности к этим величинам. На рис. 7÷10
представлены аппроксимации долготных и широтных невязок вычисленные по множеству
зодиакальных звезд и всех звезд каталога.

Рис. 7. Систематическая ошибка в долготе определенная по множеству зодиакальных звезд.

Рис. 8. Систематическая ошибка в долготе определенная по множеству всех звезд.

Рис. 9. Систематическая ошибка в широте определенная по множеству зодиакальных звезд.

Рис. 10. Систематическая ошибка в широте определенная по множеству всех звезд.
Для компенсации систематической ошибки по долготе получаем значение γ=11.5
±1.4 по зодиакальным звездам и γ=12.6 ±2.1 по полному множеству звезд. Значения
фаз синусоид несколько отличны друг от друга и составляют соответственно φ=53 ±9
и φ=91 ±6. Однако при реальной погрешности определения фазы в 10÷20 градусов,
доверительные диапазоны этих значений пересекаются друг с другом.
При
компенсации широтных ошибок получаем значение γ=-9.8 ±1.7 по зодиакальным
звездам и γ=-8.8 ±1.2 по полному множеству звезд. Значения фаз синусоид
составляют соответственно φ=33 ±9 и φ=61 ±8.
Устраним систематические долготные и широтные ошибки с помощю компенсационой
синусоиды, с параметрами γ и φ, которые соответствуют полному множеству звезд.
После этого определим остаточные ошибки в координатах звезд и вычислим в первом
приближении среднеквадратичную ошибку, которая составит 29' для долготы и 27'
для широты. Реальная точность измерения координат несколько выше, и для её
нахождения необходимо устранить выбросы. Выбросом будем считать такое измерение,
при котором значение невязки не укладывается в удвоенный диапазон найденной
среднеквадратичной ошибки, которые составляют 58' для долготы и 54' для
широты.
Повторяя всю процедуру расчета, находим значения среднеквадратчных
ошибок, которые составят 23' долготы и 21' для широты. Полученные значения
случайных ошибок измерения примерно соответствуют точности звездного каталога
"Альмагест". Поскольку точность измерения координат звезд в каталогах Птолемея и
Улугбека совпадает, а состав быстрых звезд одинаков, точность (погрешность)
определения датировки этих каталогов должна быть примерно одинаковой.
Датировка каталога Улугбека методом Дамбиса-Ефремова.
В качестве первого приближения будем использовать число звезд сравнения Nref=6. Такой выбор мотивируем следующими факторами. Как было показано на рис.5 при большом числе Nref явного минимума остаточной невязки нет ни по долготе, ни по широте. Поскольку, для датировки обоих каталогов используются одни и те же звезды (за исключением нескольких плохо измеренных), и каталоги имеют примерно одинаковые ошибки измерения, мы вправе ожидать, что остаточные суммарные невязки звезд каталога Улугбека будут столь же слабо зависеть от числа Nref, как и в "Альмагесте". Именно поэтому для первичного расчета возьмем число звезд сравнения Nref=6, которое используют в своих расчетах А.К. Дамбис и Ю.Н. Ефремов. В дальнейшем, можно провести расчеты с другим числом Nref и исследовать на устойчивость полученный результат.
Вариант Nref=6
Для датировки каталога будем использовать все звезды проекции которых по долготе или широте превышают 0.45"/год. Если проекция скорости по одной из координат меньше этого значения, то данная проекция не будет учитываться при вычислении датировки. Заметим, что в своем варианте расчета А.К. Дамбис и Ю.Н. Ефремов используют обе компоненты скорости звезды даже в том случае, когда скорость по медленной компоненте близка к нулю (например, проекция скорости Арктура по долготе). Хотя медленная компонента скорости практически не оказывает влияния на центр датировки, на наш взгляд её включение в датировку является методической ошибкой, поскольку в этом случае, авторам следовало бы включить в датировку все звезды с аналогичной по величине скоростью. Это можно было бы сделать, однако в этом случае остаточная невязка звезды будет обусловлена не собственным движением, а случайной ошибкой измерения, что не имеет смысла.Из общего множества быстрых звезд исключим звезды, невязки координат которых не соответствуют невязкам координат звезд из ближайшей окрестности, рис. 11.

Рис. 11. Распределение быстрых звезд каталога Улугбека в координатах "скорость-невязка окрестности".
Широтные невязки звезд ο2 Эридана (Кейд), δ и τ6
Эридана, а так же долготные невязки β и γ Девы, ε Скорпиона не попадают в
интервал ошибки 2σ, который составляет 46' для долготы и 42' для широты.
Указанные координаты звезд являются ошибками измерения, и поэтому, непригодны
для датировки при значениях Nref от 4 до 10. Расчет показывает, что
невязки всех перечисленных звезд кроме Кейда не попадают в удвоенный интервал
ошибки измерения. Широтная невязка Кейда начинает уменьшаться с ростом радиуса
окрестности, при радиусе окрестности R=10° составляет около +1.5°, а при R=14°
уменьшается до 40' и попадает в интервал удвоенной ошибки измерения. Однако
понятно, что набираемые при этом удаленные звезды сравнения не имеют никакого
отношения к групповой ошибке окрестности Кейда, поэтому составлять столь
протяженные окрестности сравнения не имеет смысла.
Заметим, что долготная
невязка Кейда укладывается в пределы случайной ошибки измерения, поэтому будет
использоваться при дальнейших расчетах. В интервал удвоенной ошибки измерения
так же не попадает невязка долготной проекции γ Змеи (оранжевый кружок), которая
составляет 48', поэтому мы не будем включать эту звезду в основной расчет.
Однако, учитывая, что сами значения случайных ошибок измерения определены с
некой погрешностью, включим проекцию долготы γ Змеи в дополнительный расчет хотя
бы для исследования результата на устойчивость.
Заметим, в отличие от А.К.
Дамбиса и Ю.Н. Ефремова мы построили зависимость по оси Х только от проекции
собственной скорости звезды μ, а не от разности собственной скорости μ и средней
скорости окрестности <μneib>. При использовании быстрых звезд
поправка скорости, которую может обеспечить окрестность довольно мала и
действует одинаково (в подавляющем большинстве случаев приводит к уменьшению
скорости звезды). Кроме того, такая поправка будет незначительна, если
предполагаемая расчетная дата примерно соответствует реальной дате составления
каталога. Наконец, проблема учета скорости окрестности несколько некорректна:
поскольку ошибка окрестности считается по медиане, она определится по невязкам
одной или двух звезд, которые могут иметь совсем разные скорости, несовпадающие
со скоростями остальных звезд окрестности. Поэтому, вычисление средней скорости
окрестности по части ее звезд и подсчете по медиане вносит произвол.
После формирования множества быстрых звезд на основании которого будет
определяться датировка и установив число звезд сравнения в окрестности быстрой
звезды, вычислим промежуточные датировки по проекции долготы и широты. Значения
коэффициентов регрессий составит kλ=1.42 ±2.18 и kβ=-6.72
±3.12, которые можно перевести к календарной дате Т = 1437 +60•k. Отсюда,
получаем Tλ=1522 год ±131 год и Tβ=1034 год ±187 лет.
Таким образом, центры датировок по долготам и широтам разошлись на 488 лет и при
этом, погрешности датировок не пересекаются.
Поскольку результат датировки
может значительно зависеть от нескольких наиболее быстрых звезд, проведем
дополнительное исследование на устойчивость коэффициента наклона регрессии. Для
этого будем последовательно исключать из датировки проекции скоростей наиболее
быстрых звезд. Результат такого исследования представлен на рис. 12.

Рис. 12. Усточивость коэффициентов наклона регрессий Tλ, Tβ при исключении быстрых звезд каталога.
На рисунке 12 сплошной жирной чертой обозначена дата составления каталога
Улугбека 1437 год, которому соответствует коэффициент наклона регрессии k=0.
Красной жирной чертой с пустыми ромбами обозначеная зависимость коэффициента
наклона регрессии kλ, тонкой чертой обозначен возможный интервал
датировок при уровне доверия 2σ. Темно-синим цветом обозначены аналогичные
величины для коэффициента kβ.
Из представленного рисунка следует,
что центры датировок весьма слабо изменяются при удалении из выборки пяти звезд
с самыми быстрыми проекциями скоростей по долготе и широте. Среднее значение
коэффициента для долготной регрессии составит kλ=2.74 и для широтной
регрессии kβ=-6.7. Заметим, что доверительные интервалы коэффициентов
регрессий (=датировки) начинают пересекаться только при исключении десяти
наиболее быстрых проекций скоростей (включая ε Эридана и 36 Змееносца), причем
пересечение происходит при ширине доверительного интервала 2σ. Для того, чтобы
получить согласование коэффициентов при ширине доверительного интервала в σ
необходимо удалить из выборки еще несколько быстрых звезд. Содержательного
смысла эта процедура не несет, поскольку положение центров будет меняться при
исключении звезд слабо, а пересечение доверительных интервалов будет достигнуто
только по причине удаления части данных, что и приводит к увеличению
погрешности. Таким образом, расчет датировок Тλ и Тβ по
проекциям скоростей показал их существенное расхождение, которое является
следствием либо заниженной погрешности каждой из частных датировок, либо
ошибочным определением центров датировок, но наиболее вероятным вариантом
является наличие обоих упомянутых факторов.
Вычислим смешанную датировку
Тλβ снова взяв в качестве предполагаемой даты составления каталога
1437 год, рис.13.

Рис. 13. Датировка каталога Улугбека при Nref=6.
В основном варианте, значение коэффициента наклона регрессии заключено в диапазоне значений Тλβ =-4.8÷-2.7, что соответствует календарным датам составления каталога 1149÷1275 гг. Однако, соответствие традиционной дате каталога достигается только при удалении из рассмотрения семи наиболее быстрых звезд включая ι Персея.
Вариант Nref=6 + γ Змеи
Проведем еще один вариант расчета датировки при Nref=6, но с учетом долготной проекции звезды γ Змеи. С формальной точки зрения эта звезда не должна присутствовать в расчете, поскольку её невязка отличается от невязки окрестности на 52' при допуске 48'. Тем не менее, расчет датировки с учетом долготной проекции γ Змеи интересен сразу по двум причинам. Невязка данной звезды находится на грани попадания в удвоенный доверительный интервал при Nref=4 и Nref=6 и попадает в него при Nref=8. Вызывает интерес вопрос устойчивости центра датировки от такой звезды и её влияние на погрешность датировки.
Рис. 14. Датировка каталога Улугбека при Nref=6 с включением γ Змеи.
Согласно проведенному расчету включение долготной проекции γ Змеи оказывает заметное влияние на результат датировки поскольку среднее значение коэффициента наклона регрессии изменяется на Δk=1.11 при том, что скорость данной звезды по долготе относительно невелика (~0.65"/год). Погрешность датировки возрастает на 15%, а центр датировки смещается таким образом, что традиционная дата составления каталога не соответствует дате составления каталога даже с учетом возросшей погрешности.
Вариант Nref=4
Рассмотрим датировку каталога при котором окрестность сравнения будет состоять всего из четырех звезд, то есть Nref=4. Для этого, как и в предыдущем расчете определим частные датировки по проекциям Tλ, Tβ, а потом полную датировку Tλβ рис. 15, 16.
Рис. 15. Частные датировки Tλ, Tβ при Nref=4
В данном варианте расчета частные датировки Tλ, Tβ соответствуют лучше друг другу, чем в предыдущем случае при Nref=6, поскольку уже при исключении ο2 Эридана доверительные интервалы частных датировок начинают пересекаться. Однако центры частных датировок по прежнему смещены друг от друга на ~400 лет, а пересечение доверительных интервалов обеспечивается возросшим значением (по сравнению с Nref=6) погрешности датировок.

Рис. 16. Датировка каталога Улугбека при Nref=4
Смешанная датировка Tλβ при исключении ο2 Эридана и α Волопаса соответствует традиционной дате составления каталога на уровне доверия 2σ, а при исключении пяти наиболее быстрых звезд центр датировки смещается в начало 15 века.
Вариант Nref=8
Рассмотрим вариант датировки при котором окрестность сравнения будет состоять из восьми звезд, Nref=8. Вычислим частные датировки определим по проекциям Tλ, Tβ и полную датировку Tλβ рис. 17, 18.
Рис. 17. Частные датировки Tλ и широтам Tβ при Nref=8.
Коэффициенты наклона регрессий заключены в диапазонах от kλ=+0.4÷-2.0 и kβ= -4.8÷-7.8, что дает средние значения kλср=-1.1 и kbeta;ср=-6.1. В данном варианте частные датировки ближе всего приблизились друг к другу, а поэтому доверительные диапазоны датировок пересекаются во всех вариантах при исключении проекции Кейда и Арктура.
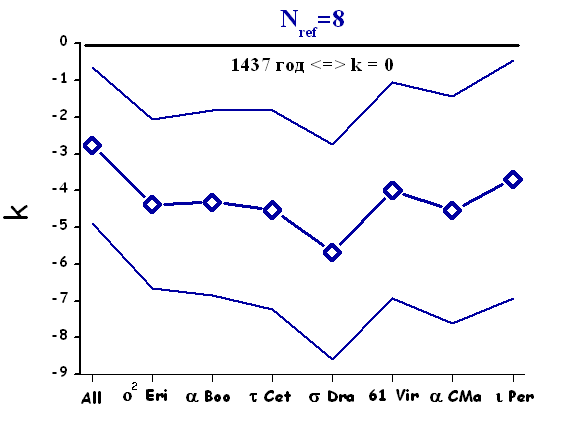
Рис. 18. Датировка каталога Улугбека при Nref=8.
На рисунке 18 представлена датировка Tλβ при Nref=8. Ни один из вариантов не соответствует традиционной дате составления каталога. Значение kλβ слабо зависит при исключении звезд и заключено в диапазоне -2.8÷-5.8 при среднем значении kλβср=-4.1. Погрешность датировки медленно возрастает с исключением звезд и лишь этим фактором обусловлено попадание традиционной даты составления каталога в доверительный интервал датировки.
Вариант при больших значениях Nref
При значении Nref=10 радиус окрестности в половине окрестностей составляет 11÷13 градусов, а в каждой шестой окрестности превышает это значение. Можно ограничить радиус окрестности 14 градусами и рассмотреть этот вариант как предельный. Однако и в этом случае kλβ составит в различных вариантах от -4 до -8 при исключении самых быстрых звезд. Впрочем этот результат нельзя считать надежным, поскольку в окрестность быстрой звезды набираются звезды с совсем отличной систематикой. В частности, в датировку добавляется широтная компонента звезды ο2 Эридана, которая значительно удревняет датировку. Широтная проекция этой звезды не попала ни в один из предыдущих вариантов расчета поскольку широтная невязка звезды не соответствует широтной невязки окрестности. Однако, при радиусе окрестности R=14° в окрестность начинают набираться звезды с совершенно разной групповой ошибкой, что в данном случае приводит к разнице невязок Кейда и окрестности до +40'. Этот эффект наблюдается в большинстве окрестностей, что приводит в одних случаях к удревнению датировки, а в других к её омоложению.Анализ результатов датировки
Подведем итоги датировки звездного каталога Улугбека с помощью коллективного
метода. Расчеты при Nref=6, Nref=8 и
Nref=Nref(Rокр=14°) показывают, что каталог был
составлен в более древнюю эпоху. И только расчет при Nref=4 при
удалении нескольких быстрых звезд оставляет надежду на то, коллективный метод
способен давать адекватный результат, который соответствует традиционной дате
составления каталога. Таким образом, для принятия окончательного решения о
пригодности метода необходимо корректно выделить какой из вариантов датировки
является наиболее точным.
Сразу же заметим, что к варианту расчета с
Nref=4 есть два замечания. Во-первых, невязка окрестности
определяется по медиане, которая применима при гауссовом распределении ошибки, и
большом числе проб. Однако, при малом числе звезд Nref=4
распределение невязок звезд окрестности может значительно отличаться от
распределения Гаусса, а сам результат не будет защищен от влияния выбросов. Этот
фактор приводит к тому, что результирующая невязка звезд окрестности будет
определена некорректно. Во-вторых, было бы несколько странным предположить, что
дата составления каталога может быть получена только в результате одного расчета
(да еще с удалением части звезд), а все остальные расчеты дают явно ошибочные
результаты. Этих двух соображений вполне достаточно, чтобы забраковать расчет
при Nref=4.
Однако, провести выбор оптимального варианта можно с помощью математических критериев, если для каждого варианта расчета определить значение χ2. Фактически, параметр χ2 является индикатором того насколько плотно (кучно) остаточные невязки (разница невязки быстрой звезды и ее окрестности) сгруппированы около регрессионной прямой. Меньшие значения χ2 соответствуют меньшим средним значениям остаточных невязок, что означает лучшее соответствие между невязкой звезды и невязкой её окрестности. Это можно использовать в качестве критерия при выборе оптимального значения Nref, рис. 19.
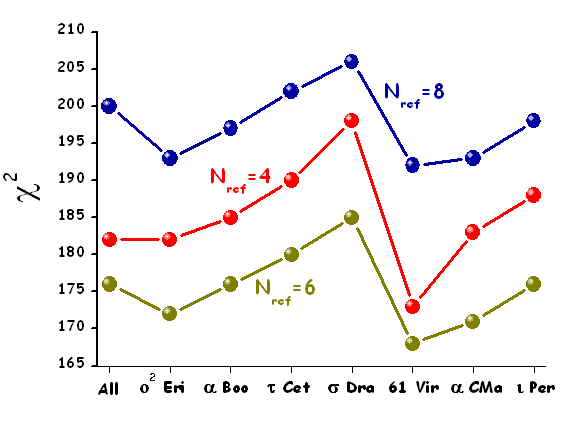
Рис. 19. Поведение параметра χ2 при разном числе звезд сравнения.
Из рисунка следует, что наименьшим значениям величины χ2 соответствует вариант расчета при Nref=6, в то время как варианты с Nref=4 и Nref=8 имеют более высокие значения χ2. Поэтому, окрестность из 6 звезд сравнения является наиболее предпочтительной с формальной точки зрения. Относительно высокие значения χ2 в других вариантах вероятно обусловлены некорректным использованием усреднения по медиане (вариант при Nref=4) и набором в окрестность звезд с различной групповой ошибкой (вариант при Nref=8). Расчеты с нечетным значением Nref=5 и Nref=7 так же дают большие значения параметра χ2, однако этот результат был ожидаем, поскольку при малом числе проб медиана чаще более точна при нечетном числе испытаний.

Рис. 20. Поведение параметра χ2 при Nref=6 с учетом γ Змеи.
Расчет с Nref=6 при учете непопадающей в интервал 2σ γ Змеи
приводит к значительному росту параметра χ2, причем, даже если бы эта
звезда попадала в необходимый интервал величина χ2 незначительно. При
добавлении в расчеты с Nref=4 и Nref=6 звезды γ Змеи,
которая участвует в расчете с Nref=8 оптимальным по параметру
χ2 становится вариант с Nref=8.
В связи с этим, очень
интересно замечание высказанное Д.Дъюком о том, что А.К. Дамбис и Ю.Н. Ефремов
исключили из расчета широтную проекцию звезды θ Центавра, невязка которой
попадает в интервал 2.5σ [2], хотя изначально был заявлен доверительный интервал
в интервал 3σ. Заметим, что по величине широтная компонента скорости θ Центавра
имеет примерно такое же значене, что и долготная компонента скорости γ Змеи.
Поэтому, добавление звезды θ Центавра в расчет А.К. Дамбиса и Ю.Н. Ефремова не
только омолодит датировку, но и увеличит значение погрешности датировки на
15÷30% (несколько вариантов датировок при последовательном исключении быстрых
звезд), что сделает невозможным установления авторства каталога между Гиппархом
и Птолемеем даже оставаясь в рамках метода А.К. Дамбиса и Ю.Н. Ефремова.
Вывод.
Минимальное значение критерия χ2 соответствует расчету при котором окрестность состоит из шести звезд сравнения, т.е. Nref. однако результат датировки при Nref=6 который дает "коллективный" метод А.К. Дамбиса и Ю.Н. Ефремова не соответствует с учетом погрешности традиционной дате составления каталога, что является подтверждением высказанных нами тезисов о недостаточной точности и корректности данного метода.Заключение
1. Датировка звездного каталога Улугбека, проведенная по "коллективному" методу А.К. Дамбиса и Ю.Н. Ефремова при различном числе звезд сравнения не соответствует с учетом погрешности общепринятой дате составления каталога. Из этого результата следует альтернатива: либо звездный каталог Улугбека был составлен на 200÷300 лет раньше традиционного срока, либо недостаточно корректен и точен используемый для датировки метод. Возможные причины некорректности "коллективного" метода были сформулированы в замечаниях 1÷6. Совокупность этих факторов приводит к недооценке погрешности датировки, неправильному вычислению центра датировки, что подтверждается численным расчетом.2. При датировке звездного каталога "Альмагест" "коллективным" методом возможны еще большие отклонения центра датировки от истинной даты составления каталога, которые обусловлены более высокими значениями систематических ошибок и наличием в каталоге "Альмагеста" разных систематик [6]. В звездном каталоге Улугбека систематические ошибки около 2 раз меньше чем в "Альмагесте", и главное, они описываются единой систематической ошибкой. Иcходя из этих соображений, "Альмагест" датируется "коллективным" методом еще менее точно, чем каталог Улугбека, однако дать этому точную количественную оценку невозможно.
3. Результат датировки звездного каталога "Альмагест" "коллективным" методом А.К. Дамбиса и Ю.Н. Ефремова является недостоверным. Данный метод не только не позволяет установить принадлежность авторства каталога между Гиппархом (-130 г. до н.э.) и Птолемеем (130 г. н.э.), но не исключает возможность составления каталога в более раннюю или позднюю эпоху.
Литература
1) А.К. Дамбис, Ю.Н. Ефремов Датировка звездного каталога Птолемея по собственным движениям: тысячелетняя проблема решена. // Историко-астрономические исследования, вып. XXVI, стр. 7-25, Mосква "Наука", 2001.
2) D.W. Duke Dating tha Almagest star catalogue using propper motions: a reconsideration.
3) Улугбек Зидж (под редакцией А. Ахметова), Ташкент, 1994.
4) С. Peters, Е. Knobel Ptolemy's сatalogue of stars a revision of the Almagest // Washington, 1915.
5) Р. Ньютон Преступление Клавдия Птолемея
6) В.В. Калашников, Г.В. Носовский, А.Т. Фоменко Датировка звёздного каталога «Альмагеста». Статистический и геометрический анализ, Москва, Факториал, 1995
7) Центр астрономических данных в Страсбурге
8) В.Е. Жаров Сферическая астрономия, Москва, 2002.
9) O. Montenbuck, T. Peleger Astronomy on the Personal Computer, Springer, 2003.
